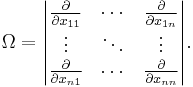Cayley's Ω process

In mathematics, Cayley's Ω process, introduced by Arthur Cayley (1846), is a relatively invariant differential operator on the general linear group, that is used to construct invariants of a group action.

As a partial differential operator acting on functions of n² variables x_ij, the omega operator is given by the determinant

$\Omega = \begin{vmatrix} \frac{\partial}{\partial x_{11}} & \cdots &\frac{\partial}{\partial x_{1n}} \\ \vdots& \ddots & \vdots\\ \frac{\partial}{\partial x_{n1}} & \cdots &\frac{\partial}{\partial x_{nn}} \end{vmatrix}.$

Applications

Cayley's Ω process appears in Capelli's identity, which Weyl (1946) used to find generators for the invariants of various classical groups acting on natural polynomial algebras.

Hilbert (1890) used Cayley's Ω process in his proof of finite generation of rings of invariants of the general linear group. His use of the Ω process gives an explicit formula for the Reynolds operator of the special linear group.

Cayley's Ω process is used to define transvectants.

References

Cayley, Arthur (1846), "On linear transformations", Cambridge and Dublin mathematical journal 1: 104–122, http://books.google.com/books?id=PBcAAAAAMAAJ&dq=Cambridge%20and%20Dublin%20mathematical%20journal%201846&pg=PR3#v=onepage&q=Cambridge%20and%20Dublin%20mathematical%20journal%201846&f=false Reprinted in Cayley (1889), The collected mathematical papers, 1, Cambridge: Cambridge University press, pp. 95–112
Hilbert, David (1890), "Ueber die Theorie der algebraischen Formen", Mathematische Annalen 36 (4): 473–534, doi:10.1007/BF01208503, ISSN 0025-5831
Howe, Roger (1989), "Remarks on classical invariant theory.", Transactions of the American Mathematical Society (American Mathematical Society) 313 (2): 539–570, doi:10.1090/S0002-9947-1989-0986027-X, ISSN 0002-9947, JSTOR 2001418, MR 0986027
Olver, Peter J. (1999), Classical invariant theory, Cambridge University Press, ISBN 978-0-521-55821-1
Sturmfels, Bernd (1993), Algorithms in invariant theory, Texts and Monographs in Symbolic Computation, Berlin, New York: Springer-Verlag, ISBN 978-3-211-82445-0, MR 1255980
Weyl, Hermann (1946), The Classical Groups: Their Invariants and Representations, Princeton University Press, ISBN 978-0-691-05756-9, MR 0000255, http://books.google.com/?id=zmzKSP2xTtYC, retrieved 03/2007/26